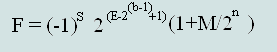 (Формула №1)
(Формула №1)
 Главная
Назад
Главная
Назад
Автор: Яшкардин Владимир
www.softelectro.ru
Дата: 2009
Редакция: 04.06.2012
info@softelectro.ru
Данный стандарт разработан ассоциацией IEEE (Institute of Electrical and Electronics Engineers) и используется для представления действительных чисел (чисел с плавающей точкой) в двоичном коде. Наиболее используемый стандарт для вычислений с плавающей точкой, используется многими микропроцессорами и логическими устройствами, а также программными средствами.
В 2008 года ассоциация IEEE выпустила стандарт IEEE 754-2008, который включил в себя стандарт IEEE 754-1985.
Стандарт содержит 23 страницы текста в 7 секциях и одном приложении:
К сожалению, организация IEEE превратилась из международной общественной инженерной организации (которой она была изначально) в торговую организацию.
Этой организации принадлежит авторское право на публикацию стандарта IEEE754-1985.
Поэтому если вы захотите ознакомиться, с оригиналом стандарта, вам придется купить его примерно за 80$.
Но, Российского законодательство разрешает мне в учебных целях комментировать данный стандарт.
Поэтому дальше я буду давать вольное изложение стандарта и выражать своё мнение о нём в учебных целях.
Возьмем, к примеру, десятичное число 155,625
Представим это число в нормализованном экспоненциальном виде : 1,55625∙10+2=1,55625∙exp10+2
Число 1,55625∙exp10+2 состоит из двух частей: мантиссы M=1.55625 и экспоненты exp10=+2
Если мантисса находится в диапазоне 1<=M<10, то число считается нормализованным.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае +2).
Порядок экспоненты может иметь отрицательное значение, например число 0,0155625=1,55625∙exp10-2.
Возьмем, к примеру, десятичное число 155,625
Представим это число в денормализованном экспоненциальном виде : 0,155625∙10+3=0,155625∙exp10+3
Число 0,155625∙exp10+3 состоит из двух частей: мантиссы M=0,155625 и экспоненты exp10=+3
Если мантисса находится в диапазоне 0,1<=M<1, то число считается денормализованным.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае +3).
Порядок экспоненты может иметь отрицательное значение, например число 0,0155625=0,155625∙exp10-3.
Наша задача сводится к представлению десятичного числа с плавающей точкой, в двоичное число с плавающей точкой в экспоненциальном нормализованном виде. Для этого разложим заданное число по двоичным разрядам:
155,625 = 1∙27 +0∙26+0∙25+1∙24+1∙23+0∙22+1∙21+1∙20+1∙2-1+0∙2-2+1∙2-3
155,625 =128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0,5 + 0 + 0,125
155,62510 = 10011011,1012 - число в десятичной и в двоичной системе с плавающей точкой
Приведем полученное число к нормализованному виду в десятичной и двоичной системе:
1,55625∙exp10+2 = 1,0011011101∙exp2+111
Основное применение в технике и программирование получили форматы 32 и 64 бита.
Например, в VB используют типы данных single (32 бита) и double (64 бита).
В Си аналогично используют float (32 бита) и double (64 бит)
Рассмотрим преобразование двоичного числа 10011011,101 в формат single-precision (32 бита) стандарта IEEE 754.
Остальные форматы представления чисел в IEEE 754 являются увеличенной копией single-precision.
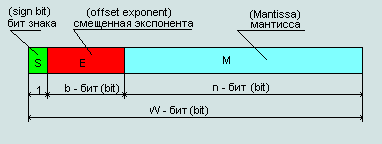
| 1 бит | 8 бит | 23 бит | IEEE 754 |
| 0 | 1000 0110 | 001 1011 1010 0000 0000 0000 | 431BA000 (hex) |
| 0(dec) | 134(dec) | 1810432(dec) | |
| знак числа | смещенная экспонента | остаток от мантиссы | число 155,625 в формате IEEE754 |
Приведём формулу для получения десятичного числа из числа IEEE754 одинарной точности:
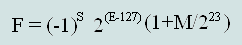 где F - десятичное число
где F - десятичное число
Проверяем наш пример:
F =(-1)0∙2(134-127)∙(1+ 1810432 / 223)= 27∙(1+0,2158203125)=128∙1,2158203125=155,625
Рис. 1 Представление числа в формате IEEE 754
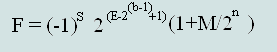 (Формула №1)
(Формула №1)
Используя формулу №1 вычислим формулы для нахождения десятичных чисел из форматов одинарной (32 бита) и двойной (64 бита) точности IEEE 754:
Рис.2 Формат числа одинарной точности (single-precision) 32 бита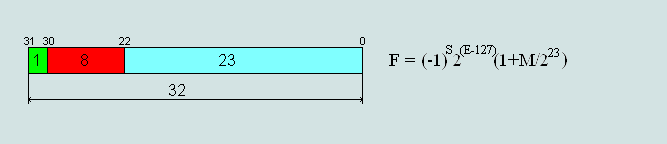
Рис.3 Формат числа двойной точности (double-precision) 64 бита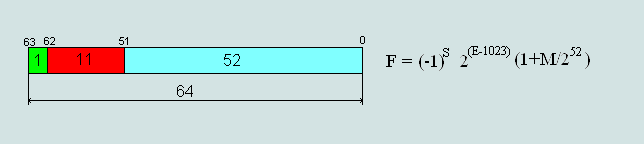
Отсюда видно, что невозможно представить число нуль или бесконечность в заданном формате.
1. число IEEE754=00 00 00 00hex считается числом +0
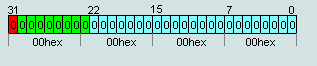
число IEEE754=80 00 00 00hex считается числом -0
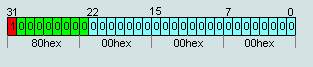
2. число IEEE754=7F 80 00 00hex считается числом +∞
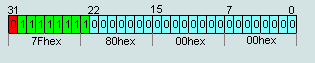
число IEEE754=FF 80 00 00hex считается числом -∞
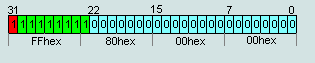
3. числа IEEE754=FF (1xxx)X XX XXhex не считается числами (NAN), кроме случая п.2
числа IEEE754=7F (1xxx)X XX XXhex не считается числами (NAN), кроме случая п.2
Число представленное в битах с 0...22 могут быть любым числом кроме 0 (т.е.+∞ и -∞ ).
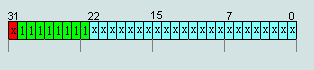
4. числа IEEE754=(x000) (0000) (0xxx)X XX XXhex считаются денормализованными числами, за исключением чисел п.1(то есть -0 и +0)
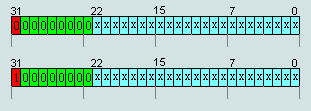
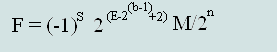 (Формула №2)
(Формула №2)
Зная формат чисел с одинарной точностью стандарта IEEE 754 можно посчитать границы диапазона представления действительных чисел в этом формате. Для этого подставим значения максимальных и минимальных абсолютных чисел IEEE 754 в формулы №1 и №2.
Минимальное нормализованное число по (абсолютное)
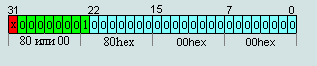
00 80 00 00 = 2-126∙(1+0/223)= 2-126 ≈ 1,17549435∙e-38
80 80 00 00 = -2-126∙(1+0/223)=-2-126 ≈ -1,17549435∙e-38
Максимальное денормализованое число (абсолютное)
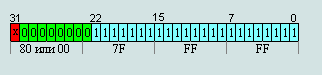
00 7F FF FF = 2-126∙(1-2-23) ≈ 1,17549421∙e-38
80 7F FF FF = -2-126∙(1-2-23) ≈ -1,17549421∙e-38
Отсюда видно что минимальное нормализированное число граничит с максимальным денормализированным.
Минимальное денормализованное число (абсолютное)
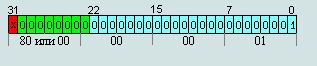
00 00 00 01 = 2-126∙ 2-23= 2-149 ≈ 1,40129846∙e-45
80 00 00 01 = -2-126∙ 2-23= 2-149 ≈ -1,40129846∙e-45
Это число граничит с нулем.
Максимальное нормализированное число (абсолютное)
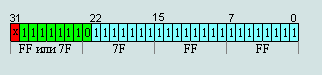
7F 7F FF FF = 2127∙(2-2-23) ≈ 3,40282347∙e+38
FF 7F FF FF = -2127∙(2-2-23) ≈ -3,40282347∙e+38
Это число граничит с бесконечностью.
Рис.4 .Диапазон чисел формата одинарной точности (32 бита) представленных по стандарту IEEE 754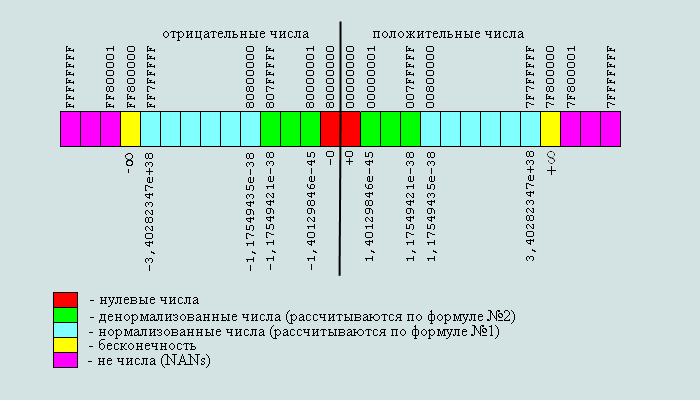
Рис.5 .Диапазон чисел формата двойной точности (64 бита) представленных по стандарту IEEE 754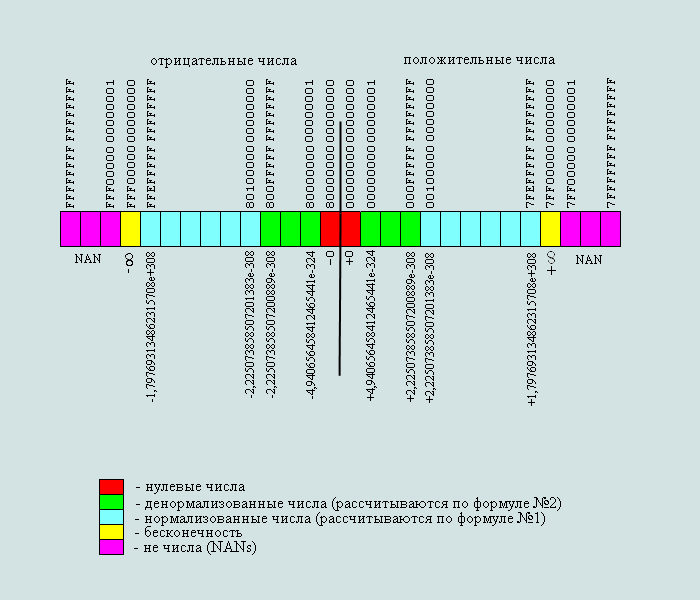
Числа представленные в формате IEEE754 представляют конечное множество, на которое отображается бесконечное множество вещественных чисел. Поэтому исходное число может быть представлено в формате IEEE754 с ошибкой.
Рис.6 Функция ошибки точности представления числа в IEEE754 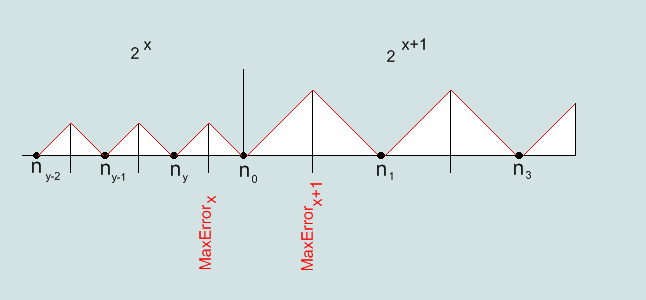
Абсолютная максимальная ошибка для числа в формате IEEE754 равна в пределе половине шага чисел.
Шаг чисел удваивается с увеличением экспоненты двоичного числа на единицу.
То есть, чем дальше от нуля, тем шире шаг чисел в формате IEEE754 по числовой оси.
Шаг денормализованных чисел равен 2(E-149) (Single) и 2(E-1074) (Double).
Соответственно предел макс. абсолютной ошибки будет равен 1/2 шага числа: 2(E-150) (Single) и 2(E-1075) (Double).
Относительная ошибка в % будет равна: (2(E-150)/F)*100%(Single) и (2(E-1075)/F)*100% (Double).
Шаг нормализованных чисел равен 2(E-150) (Single) и 2(E-1075) (Double).
Соответственно предел макс. абсолютной ошибки будет равен 1/2 шага числа: 2(E-151) (Single) и 2(E-1076) (Double).
Относительная ошибка в % будет равна: (2(E-151)/F)*100%(Single) и (2(E-1076)/F)*100% (Double).
Максимальная относительная ошибка для денормализованного числа(single/double): 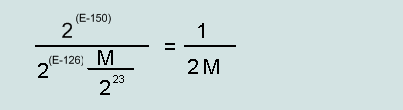
Максимальная относительная ошибка нормализованного числа(single): 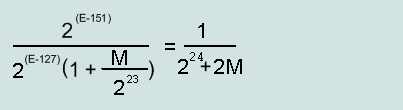
Максимальная относительная ошибка нормализованного числа(double): 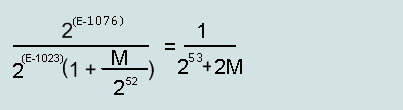
| IEEE754, hex | число, dec | абсолютная ошибка, dec | относительная, % |
| 00000001 | 2-149 ≈1,401298e-45 | 2-150≈0,700649e-45 | =50 |
| 00000002 | 2-148 ≈2,802597e-45 | 2-150≈0,700649e-45 | =25 |
| 00000032 | ≈7,00649e-44 | 2-150≈0,700649e-45 | =1 |
| 007FFFFF | ≈1,175494e-38 | 2-150≈0,700649e-45 | ≈5,96e-6 |
| 00800001 | ≈1,175494e-38 | 2-149 ≈1,401298e-45 | ≈11,9209e-6 |
| 0DA24260 | ≈1,0e-30 | 2-123 ≈9,4039e-38 | ≈9,4039e-6 |
| 1E3CE508 | ≈1,0e-20 | 2-90 ≈8,0779e-28 | ≈8,0779e-6 |
| 2EDBE6FF | ≈1,0e-10 | 2-57 ≈6,9389e-18 | ≈6,9389e-6 |
| 3F800000 | ≈1,0 | 2-23 ≈1,192e-7 | ≈11,9209e-6 |
| 41200000 | ≈10,0 | 2-20 ≈9,5367e-7 | ≈9,5367e-6 |
| 42C80000 | ≈1,0e+2 | 2-17 ≈7,6294e-6 | ≈7,62939e-6 |
| 501502F9 | ≈1,0e+10 | 210 ≈1,024e+3 | ≈10,24e-6 |
| 60AD78EC | ≈1,0e+20 | 243 ≈8,7961e+12 | ≈8,7961e-6 |
| 7149F2CA | ≈1,0e+30 | 276 ≈7,5558e+22 | ≈7,5558e-6 |
| 7F7FFFFF | ≈+3,40282e+38 | 2104 ≈2,02824e+31 | ≈5,96e-6 |
| IEEE754, hex | число, dec | абсолютная ошибка, dec | относительная, % |
| 00000000 00000001 | 2-1074 ≈4,940656e-324 | 2-1075≈2,470328e-324 | =50 |
| 00000000 00000002 | 2-1073 ≈9,881313e-324 | 2-1075≈2,470328e-324 | =25 |
| 00000000 00000032 | ≈2,470328e-322 | 2-1075≈2,470328e-324 | =1 |
| 000FFFFF FFFFFFFF | ≈2,225073e-308 | 2-1075≈2,470328e-324 | ≈1,110223e-14 |
| 00100000 00000001 | ≈2,225074e-308 | 2-1074 ≈4,940656e-324 | ≈2,220446e-14 |
| 2B2BFF2E E48E0530 | ≈1,0e-100 | 2-385 ≈1,268971e-116 | ≈1,268971e-14 |
| 3FF00000 00000000 | =1,0 | 2-52 ≈2,220446e-16 | ≈2,220446e-14 |
| 54B249AD 2594C37D | ≈1,0e+100 | 2280 ≈1,942669e+84 | ≈1,942669e-14 |
| 6974E718 D7D7625A | ≈1,0e+200 | 2612 ≈1,699641e+184 | ≈1,699641e-14 |
| 7FEFFFFF FFFFFFFF | ≈1,79769e+308 | 2971 ≈1,99584e+292 | ≈1,110223e-14 |
Из выше приведенного следует, что основная масса чисел в формате IEEE754 имеет стабильную небольшую относительную погрешность:
Максимально возможная относительная погрешность для числа Single составляет 2-23*100% =11,920928955078125e-6 %
Максимально возможная относительная погрешность для числа Double составляет 2-52*100% =2,2204460492503130808472633361816e-14 %
| наименование формата | single-precision | double-precision |
| длина числа, бит | 32 | 64 |
| смещенная экспонента (E), бит | 8 | 11 |
| остаток от мантиссы (M), бит | 23 | 52 |
| смещение | 127 | 1023 |
| двоичное денормализованое число | (-1)S∙0,M∙exp2-127 ,где M-бинарное | (-1)S∙0,M∙exp2-1023 ,где M-бинарное |
| двоичное нормализованое число | (-1)S∙1,M∙exp2(E-127) ,где M-бинарное | (-1)S∙1,M∙exp2(E-1023) ,где M-бинарное |
| десятичное денормализованное число | F =(-1)S∙2(E -126)∙ M/223 | F =(-1)S∙2(E -1022)∙M/252 |
| десятичное нормализованное число | F =(-1)S∙2(E-127)∙(1+ M/223) | F =(-1)S∙2(E-1023)∙(1+M/252) |
| Абс. макс. возм. погрешность числа | 2(E-150) | 2(E-1075) |
| Отн. макс. возм. погрешность денорм. числа | 1/(2M) | 1/(2M) |
| Отн. макс. возм. погрешность норм. числа | 1/(224+2M) | 1/(253+2M) |
| минимальное число | ±2-149≈ ±1,40129846∙e-45 | ±2-1074≈ ± 4,94065646∙e-324 |
| максимальное число | ±2127∙(2-2-23) ≈ ± 3,40282347∙e+38 | ±21023∙(2-2-52) ≈ ± 1,79769313∙e+308 |
Стандарт IEEE754 предусматривает четыре способа округления чисел.
| исходное число | к ближ. целому | к нулю | к +∞ | к -∞ |
| 1,33 | 1,3 | 1,3 | 1,4 | 1,3 |
| -1,33 | -1,3 | -1,3 | -1,3 | -1,4 |
| 1,37 | 1,4 | 1,3 | 1,4 | 1,3 |
| -1,37 | -1,4 | -1,3 | -1,3 | -1,4 |
| 1,35 | 1,4 | 1,3 | 1,4 | 1,3 |
| -1,35 | -1,4 | -1,3 | -1,3 | -1,4 |
Как происходит округление показано на примерах в таблице 3. При преобразовании чисел необходимо выбрать один из способов округления. По умолчанию это первый способ -округление к ближайшему целому. Часто в различных устройствах используют второй способ - округление к нулю. При округлении к нулю нужно просто отбросить не значащие разряды числа, поэтому этот способ самый легкий в аппаратной реализации.
Стандарт IEEE 754 широко применяется в технике и программировании.
Большинство современных микропроцессоров изготовляются с аппаратной реализацией представления вещественных переменных в формате IEEE754.
Язык программирования и программист не могут изменить эту ситуацию, иного преставления вещественного числа в микропроцессоре не существует.
Когда создавали стандарт IEEE754-1985 представление вещественной переменной в виде 4 или 8 байт казалось очень большой величиной, так как объём оперативной памяти MS-DOS был равен 1 Мб.
А, программа в этой системе могла использовать только 0,64 Мб.
Для современных ОС размер в 8 байт является ничтожным, тем не менее переменные в большинстве микропроцессоров продолжают представлять в формате IEEE754-1985.
Рассмотрим ошибки компьютерных вычислений, вызванные применением чисел в формате IEEE754.
Данная ошибка всегда присутствую в компьютерных вычислениях.
Причина её возникновения описана в п.7.4.
Радует только то, что величина относительной ошибки имеет размерность для single 10-6 для double 10-14
Величины абсолютных ошибок могут быть значительными, максимально для single 1031 и для double 10292, что может вызывать определённые проблемы вычислений.
//Пример 1. Ошибка вызванная точностью представления числа в формате IEEE754
#include "stdio.h"
int
main(int argc, char *argv[])
{
float a, b, f;
a=123456789;
b=123456788;
f=a-b;
printf("Result: %f\n", f);
return 0;
}
Result: 8.000000 (Ответ должен быть 1.000000)
Если пример посчитать на бумажке, то ответ будет 1. Абсолютная ошибка равна +7.
Почему ответ получился неправильным?
Число 123456789 в single=4CEB79A3hex(ieee)=123456792(dec) абсолютная ошибка представления равна +3
Число 123456788 в single=4CEB79A2hex(ieee)=123456784(dec) абсолютная ошибка представления равна -4
Относительная погрешность исходных чисел приблизительно равна 3,24e-6%
В результате одной операции относительная погрешность результата стала 800%, т.е. увеличилась в 2,5e+8 раз.
Это я называю "Опасной редукцией", т.е. катастрофическим понижением точности вычислений в операция где абсолютное значение результата много меньше любого из входного значения переменных.
На самом деле ошибки точности представления числа наиболее безобидные в компьютерных вычислениях, и обычно многие программисты на них не обращают никакого внимания. Тем не менее они вас могут сильно огорчить.
Эти ошибки вызваны тем, что исходное число представленное в формате single и в формате double обычно не равны друг другу.
Например: исходное число 123456789,123456789
Single: 4CEB79A3=+123456792,0(dec)
Double: 419D6F34547E6B75=+123456789,12345679104328155517578125
Разница между Single и Double составит:2,87654320895671844482421875
Private Sub Command1_Click()
Dim a As Single
Dim b As Double
Dim c As Double
a = 123456789.123457
b = 123456789.123457
c = a - b
Text1.Text = c
End Sub
Результат: 2,87654320895672 (должен быть 0)
Относительная погрешность результата равна: ∞ (бесконечности)
Private Sub Command1_Click()
Dim a As Single
Dim b As Single
Dim c As Single
a = 123456789.123457
b = 123456789.123457
c = a - b
Text1.Text = c
End Sub
Результат: 0.0
Поэтому переменные и промежуточные результаты компьютерных вычислений должны быть приведены к одному типу данных.Обратите внимание на то, что недостаточно просто привести все исходные данные к одному типу.
Необходимо привести также результаты промежуточных операций к одному типу.
Вот пример с ошибкой в промежуточном результате:
'Пример 1 ошибка в приведении промежуточных данных на VB (Visual Studio)
Private Sub Command1_Click()
Dim a As Single
Dim b As Single
Dim c As Single
a = 1
b = 3
c = a / b
c = c - 1 / 3
Text1.Text = c
End Sub
Результат: 9,934108E-09 (Должен быть 0.0)
Здесь ошибка возникает потому, что промежуточный результат 1/3 в строке c=c-1/3 будет иметь тип double, а не single.
Чтобы избавиться от ошибки вам надо привести промежуточный результат к типу single с помощью оператора приведения типов CSng.
'Пример 2 приведение промежуточных данных на VB (Visual Studio)
Private Sub Command1_Click()
Dim a As Single
Dim b As Single
Dim c As Single
a = 1
b = 3
c = a / b
c = c - CSng(1 / 3)
Text1.Text = c
End Sub
Результат: 0.0
Пример приведения типа данных для GNU C, присланный Григорием Ситкаревым :
//Вариант 1 с не приведенным промежуточным результатом:
#include "stdafx.h"
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
int
main(int argc, char *argv[])
{
float a, b, c, d;
a = 1.0;
b = 3.0;
c = a / b;
d = (c - 1.0/3.0) * 1.0e9;//результат деления 1/3 имеет к тип double
printf("Result: %f\n", d);
return 0;
}
Result: 9.934108 (Должен быть 0.0)
//Вариант 2 с приведенным промежуточным результатом:
#include "stdafx.h"
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
int
main(int argc, char *argv[])
{
float a, b, c, d;
a = 1.0;
b = 3.0;
c = a / b;
d = (c - 1.0f/3.0f) * 1.0e9f;//результат деления 1/3 приведен к типу float
printf("Result: %f\n", d);
return 0;
}
Result: 0.0
Во втором варианте вы видите, что деление констант в промежуточном результате приведено к типу "float" (одиночная точность в Си).
Данные варианты компилировались и исполнялись с помощью "GNU C".
Если компилировать и исполнить показанные выше варианты на VC++ (Visual Studio), то результаты будут обратными.
То есть вариант 2 будет иметь результат -9.934108, а вариант 1 Result: 0.000000.
Отсюда можно сделать неутешительный вывод, что результат вычислений может зависеть от типа и версии компилятора.
В данном случае можно предположить, что компилятор VC++ автоматически приводит типы переменных, и попытка их насильственного приведения к одному типу заканчивается ошибкой.
Если Вариант 1 (без приведения типов) выполнить с переменными двойной точности (double), то ошибки приведения данных не будет и Result=0.000000
Поэтому в большинстве случаев чтобы избавиться от приведения типов данных надо просто использовать тип данных double и забыть о существовании типа single(float).
Ошибки вычислений вызванные не приведением типов данных я называю "Дикими ошибками", так как они связаны с незнанием стандартов и теории программирования (т.е. с плохим фундаментальным образованием)
1. сложение с одинаковым числом (ошибка сдвига =0.0).
2. сложение с числом меньшим в 2 раза (ошибка сдвига= - 0.00390625).
3. сложение с числом меньшим в 223 раза (ошибка сдвига= - 0.007812).
4. сложение с числом меньшим в 224 раза (ошибка сдвига= - 0.007812).
Как видно из приведенных примеров ошибка сдвига возникает если у исходных нормализованных чисел различаются экспоненты.
Если числа отличаются более чем в 223 (для single) и 252 (для double), то операции сложения и вычитания между этими числами не возможны.
Максимальная относительная погрешность результата операции равна примерно 5,96e-6%, что не превышает относительную погрешность представления числа (см.п.9.1).
Хотя с относительной погрешностью здесь всё в порядке, здесь есть другие проблемы.
Во-первых, работать с числами можно только в узком диапазоне числовой оси, где мантиссы пересекаются.
Во-вторых, для каждого исходного числа существует предел выполнения цикла называемый "Циклической дырой".
Поясню, если существует цикл в котором исходное число суммируется к сумме, то существует численный предел суммы для этого числа.
То есть сумма достигнув определённой величины перестает увеличиваться от сложения её с исходным числом.
Приведу пример циклической дыры в автоматической системе управления:
Имеется фармацевтический цех, производящий таблетки весом 10мг.
Состоящий из: формовочной машины, накопительного бункера на 500 кг, фасовочной машины, автоматической системы управления.
Формовочная машина подает в бункер по 10 таблеток одновременно.
Фасовочная машина забирает по одной таблетке.
Автоматическая система управления учитывает таблетки поступившие в бункер от формовочной машины и взятые из бункера фасовочной машиной.
То есть существует программа, которая показывает заполнения бункера продукцией в кг.
Когда в бункере будет более 500 кг продукции, формовочная машина встает на паузу , она включиться кода в бункере станет 200 кг продукции.
Фасовочная машина остановиться если в бункере будет менее 10 кг и запустится когда в бункере будет более 100 кг продукции.
Обе машины могут периодически останавливаться для обслуживания , не зависимо друг от другу (благодаря бункеру).
Как вы понимаете, такая система работает в бесконечном цикле.
Допустим в один из дней фасовочная машина простояла слишком долго и бункер заполнился до 300 кг.
Что произойдет после её включения?
Private Sub Command1_Click()
Dim a As Single 'вес таблетки в кг
Dim c As Single 'продукции в бункере в кг
Dim n As Long 'количество циклов
c = 300 'исходный вес бункера
a = 0.00001 'вес таблетки
For n = 1 To 10000000
c = c - a 'одна таблетка забирается фасовочной машиной
Next n
Text1.Text = c 'измененный вес бункера
End Sub
В данном примере фасовочная машина забрала из бункера 100 кг продукции, а вес продукции в бункере не изменился.Далее формовочная машина доведет вес бункера до 500 кг и остановится. Фасовочная машина заберет все таблетки из бункера и тоже остановится. Программа будет показывать вес в бункере 500кг. Прибегут специалисты, проверят датчики, провода, компьютер и скажут что программа зависла. Но, программа не зависала, она продолжает работать без сбоев и любой контроль это подтвердит. Просто число 0,0001 попало в циклическую дыру и выйти из него не может.
В результате нам крупно повезло, что это был фармацевтический цех, а не Саяно-Шушенская ГЭС.
На самом деле опытный программист никогда не будет делать циклическое вычитание(или суммирование) таким образом.
Этот пример вымышлен специально, и так считать нельзя, хотя с точки зрения математика здесь всё безупречно.
Эта ошибка свойственна математикам и начинающим программистам.
Я бы сказал, что основная работа программиста заключается в борьбе с погрешностями, а не в математических решениях поставленной задачи.
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
struct acc_comp {
float value;
float compens;
};
void
sub_compens(struct acc_comp *acc, float quantum)
{
float tmp, c;
tmp = quantum - acc->compens;
c = acc->value - tmp;
acc->compens = acc->value - c - tmp;
acc->value -= tmp;
}
void
sum_compens(struct acc_comp *acc, float quantum)
{
float tmp, c;
tmp = quantum - acc->compens;
c = acc->value + tmp;
acc->compens = c - acc->value - tmp;
acc->value += tmp;
}
void
sub_test()
{
struct acc_comp hopper;
struct acc_comp bunker;
float tablet;
int n, i;
n = 10000000;
hopper.value = 300.0;
hopper.compens = 0.0;
bunker.value = 0.0;
bunker.compens = 0.0;
tablet = 0.00001;
for (i = 0; i < n; i++)
{
sub_compens(&hopper, tablet);
sum_compens(&bunker, tablet);
}
hopper.value -= hopper.compens;
bunker.value += bunker.compens;
printf("Left in hopper: %04.5f kg\n", hopper.value);
printf("Held in bunker: %04.5f kg\n", bunker.value);
}
int
main(int argc, char *argv[])
{
sub_test();
return 0;
}
Показанный выше пример взят из реального промышленного кода.
#include "stdlib.h"
#include "stdio.h"
#include "math.h"
float bunker, bunker1, tablet, tablet1, compens;
long int n, i;
int
main(int argc, char *argv[])
{
tablet = 0.00001; /* вес таблетки */
tablet1 = 0.0; /* вес таблетки с учетом ошибки в предыдущих итерациях */
bunker = 300.0; /* исходный вес бункера */
bunker1 = 0.0; /* вес бункера после очередной итерации */
compens = 0.0; /* компенсация веса таблетки */
n = 10000000; /* количество циклов */
for (i = 0; i < n; i++)
{
/* вес таблетки с компенсацией ошибки */
tablet1 = tablet - compens;
/* вес бункера после вычета скомпенсированной таблетки */
bunker1 = bunker - tablet1;
/* вычисление компенсации для следующей итерации */
compens = (bunker - bunker1) - tablet1;
/* новый вес бункера */
bunker = bunker - tablet1;
}
printf("Bunker: %04.5f kg\n", bunker);
return 0;
}
Как видно из этого примера, программисту приходится вычислять погрешность результата в каждом цикле, чтобы учесть её в следующем цикле.При компьютерных вычислениях можно выделить два вида округления:
1. Результат выполненной арифметической операции всегда округляется.
2. Вывод и ввод вещественного числа в окно Windows происходит с округлением.
В первом случае переменная округляется по одному из 4-типов округления IEEE754, по умолчанию округление происходит к ближайшему целому.
При этом переменная принимает новое округлённое значение.
В п.9.2 мы рассматривали сложение двух одинаковых чисел:
1. сложение с одинаковым числом (ошибка сдвига =0.0).
Во втором случае переменная не меняет своего значения, просто в окно Windows выводится округлённое значение вещественного числа.
Получается, что исходная переменная и её отображение в окне Windows это разные числа.
Это не ошибка формата IEEE754, это ошибка Windows.
Для переменных типа Single в окне Windows отображается 7 значащих цифр округлённых до ближайшего целого.
3DFCD6EA =+0,12345679104328155517578125 в окне отображается как 0,1234568
Для переменных типа Double в окне Windows отображается 15 значащих цифр округлённых до ближайшего целого.
3FBF9ADD3746F67D=+0,12345678901234609370352046653351862914860248565673828125 отображается как 0,123456789012346
Вопрос какое значение имеет переменная когда мы вводим в окно Windows 0,123456789012346 ?
Это значение будет равно такому числу:
3FBF9ADD3746F676=+0,1234567890123459965590058118323213420808315277099609375
То есть значение переменной 3FBF9ADD3746F67D мы вообще не можем вставить напрямую в код программы.
Но, мы можем схитрить и вставить в программу x=0.123456789012346 +1E-16.
Полученная переменная будет равна 3FBF9ADD3746F67D (это используется в примере с грязным нулём)
Отобразить или вести через окно ПК такое число невозможно.
В результате действий Windows возникает ряд неприятных ситуаций.
1. У вас нет технической возможности отображать или вводить точные значения переменных в окнах, что само по себе очень печально.
2. Возникновение серьёзных ошибок, таких как грязный ноль.
"Грязный ноль" это когда вы или программа считаете, что переменная не равная нулю - равна нулю
Dim a As Double
'обнуление видимой величины
Private Sub Command1_Click()
Dim b As Double
Dim c As Double
b = Val(Replace(Text2.Text, ",", "."))
c = a - b
Text3.Text = c
End Sub
Private Sub Form_Load()
'ввод числа 3FBF9ADD3746F67D
a = 0.123456789012346 + 1E-16
Text1.Text = a
End Sub
Результат выполнения программы приведенного выше примера
В результате переменную, которую оператор считает нулем - нулю не равна
Относительная погрешность результата равна бесконечности.
В логических операциях сравнения этот не ноль может увести исполнение программы в другую ветвь алгоритма.
Эти ошибки возникают при работе с числами находящимися на границе нормализованного/денормализованного представления чисел.
Они связанны с различием в представление чисел в формате IEEE754 и в различии формул перевода формата IEEE754 в вещественные числа.
То есть устройства (или программы) должны применять различные алгоритмы в зависимости от положения вещественного числа на числовой оси формата.
Кроме того, что это приводит к усложнению устройств и алгоритмов, ещё возникает неопределённость переходной зоны.
Неопределённость переходной зоны заключается в том, что стандарт не определяет конкретного значения границы перехода.
По сути дела граница перехода находится между двумя вещественными числами:
Последним денормализованным числом 000FFFFFFFFFFFFF:
Точное десятичное значение этого числа:
+2,2250738585072008890245868760858598876504231122409594654935248025624400092282356951787758888037591552642309780950
4343120858773871583572918219930202943792242235598198275012420417889695713117910822610439719796040004548973919380791
9893608152561311337614984204327175103362739154978273159414382813627511383860409424946494228631669542910508020181592
6642134996606517803095075913058719846423906068637102005108723282784678843631944515866135041223479014792369585208321
5976210663754016137365830441936037147783553066828345356340050740730401356029680463759185831631242245215992625464943
0083685186171942241764645513713542013221703137049658321015465406803539741790602258950302350193751977303094576317321
0852507299305089761582519159720757232455434770912461317493580281734466552734375e-308
и первым нормализованным числом 0010000000000000:
Точное десятичное значение этого числа:
+2,2250738585072013830902327173324040642192159804623318305533274168872044348139181958542831590125110205640673397310
3581100515243416155346010885601238537771882113077799353200233047961014744258363607192156504694250373420837525080665
0616658158948720491179968591639648500635908770118304874799780887753749949451580451605050915399856582470818645113537
9358049921159810857660519924333521143523901487956996095912888916029926415110634663133936634775865130293717620473256
3178148566435087212282863764204484681140761391147706280168985324411002416144742161856716615054015428508471675290190
3161322778896729707373123334086988983175067838846926092773977972858659654941091369095406136467568702398678315290680
984617210924625396728515625e-308
Так как граница является вещественным числом, то её точность можно задавать до бесконечности и цифровому устройству или программе
может не хватить разрядности для принятия решения к какому диапазону отнести данное число.
Из сказанного выше видно, что мнение о том, что при вычислениях с плавающей точкой результат не выходит за пределы относительной погрешности представления наибольшего числа является ложным. Ошибки перечисленные в п.9 складываются друг с другом. Такие ошибки как грязный ноль и опасная редукция могут сделать погрешность вычислений неприемлемой. Особое внимание при программировании компьютерных вычислений программист должен обратить на результаты близкие к нулю.
Некоторые специалисты считают, что этот формат чисел представляет угрозу человечеству.
Вы можете прочитать об этом в статье IEEE754-тика угрожает человечеству
Хотя многие факты из этой статьи излишне драматизированы, и возможно неправильно интерпретированы, но проблема компьютерных вычислений философски отражена правильно.
Я не сторонник драматизации вычислений по стандарту IEEE754. Стандарт работает с 1985 года и полностью вошел в стандарт IEEE754-2008, который расширил точность вычислений. Но, проблема достоверности компьютерных вычислений сегодня очень актуальна, и стандарт IEEE754-2008 и рекомендации ISO не решили эту проблему. Я думаю, в этой области нужна инновационная идея, которой разработчики стандарта IEEE754-2008 к сожалению не обладают.
Инновационные идеи, как правило, приходят со стороны.
Основные инновационные идеи в нашем мире были выдвинуты любителями (людьми мыслящими не за деньги).
Ярким примером такой ситуации было изобретение телефона.
Когда школьный учитель Александр Белл (Alexander Graham Bell) пришел с патентом на изобретение телефона к президенту телекоммуникационной компании Western Union Company,
которая владела трансатлантическим кабелем связи, с предложением купить у него патент на изобретение телефона, он его не выгнал - нет.
Президент этой компании предложил рассмотреть этот вопрос совету экспертов в области телеграфии, состоящему из специалистов и ученых в области телекоммуникаций.
Эксперты дали заключение, что это изобретение бесполезно в области телекоммуникаций и оно бесперспективно.
Некоторые специалисты даже написали в отчете, что это циркачество и шарлатанство !
Александр Белл, вместе со своим тестем, решил самостоятельно продвигать своё изобретение.
Примерно через 10 лет, гигант телекоммуникаций Western Union Co., был фактически вытеснен телефонным бизнесом из сферы телекоммуникационных технологий .
Сегодня вы можете увидеть во многих российских городах окошки с надписью Western Union, эта компания которая занимается переводом денег по всему миру, а когда-то она была международным гигантом телекоммуникаций.
Отсюда можно сделать вывод: мнения экспертов в инновационных технологиях бесполезны!
Если Вы думает что с момента изобретения телефона (1877 г.) в головах людей что-то изменилось, то вы ошибаетесь.
Если ученые(которые придумывают новое) и специалисты (которые знают как пользоваться известным) не могут решить проблему, то нужна инновация.
Ссылки на новые идеи в области представления вещественных чисел в аппаратных средствах:
1. Аппроксиметика
2. ....?
Если вы знаете другие инновационные идей в области представления вещественных чисел, то буду рад получить ссылки на эти источники.
Можно представлять вещественные числа, как числа с фиксированной запятой.
Для представления всего диапазона чисел Double достаточно иметь переменную состоящую из 1075 битов целой части и 1075 битов дробной части, т.е. около 270 байт на одну переменную.
При этом все числа будут представлены с одинаковой абсолютной точностью.
Можно работать с числами во всем диапазоне числовой оси, то есть становится возможным суммировать большие числа с малыми числами.
Шаг чисел по числовой оси будет равномерен, то есть числовая ось будет линейна.
Тип данных будет только один, т.е. не нужны целые, вещественные и др. типы.
Здесь возникает проблема реализации регистров микропроцессоров размерностью в 270 байт, но это не проблема для современной технологии.
Для написания п.9 мне пришлось создать программу которая представляет числа в виде переменной с фиксированной точкой, длиною 1075,1075 байтов.
Где число можно представить в виде строки символов ASCII, то есть один символ равен одному числовому разряду.
Так же пришлось написать все арифметические операции при работе со строками ASCII.
Это программа является аналогом бумажного расчета. Так как математические способности микропроцессора в ней не используются, то считает она довольно медленно.
Зачем я это сделал?
Я не смог найти программы, которая смогла бы точно представить число формата IEEE754 в десятичном виде.
Так же я не нашел программы (хотя они безусловно есть, в чём нет сомнений) где в окно можно ввести 1075 значащих десятичных цифр.
Вот к примеру точно десятичное значение числа double 7FEFFFFFFFFFFFFF:
+17976931348623157081452742373170435679807056752584499659891747680315726078002853876058955
863276687817154045895351438246423432132688946418276846754670353751698604991057655128207624
549009038932894407586850845513394230458323690322294816580855933212334827479782620414472316
8738177180919299881250404026184124858368,0
Вы можете воспользоваться программой IEEE754 v.1.0
для изучения и оценки погрешностей при работе с вещественными числами представленными в формате IEEE754.
Список литературы:
1. IEEE Standard for Binary Floating-Point Arithmetic. Copyright 1985 by The Institute of Electrical and Electronics Engineers, Inc 345 East 47th Street, New York, NY 10017, USA
Благодарности:
Ситкареву Григорию Александровичу (sitkarev@komitex.ru, sinclair80@gmail.com). За помощь в создании статьи.